算法
算法
循环不变式
循环不变式(loop invariant)是一种重要的思想,用于证明一个循环的正确性。在循环开始前和结束后,循环不变式的条件必须总是成立,这是一个很强的限制条件。在循环的每个迭代中,循环不变式还应该保持成立,这是循环不变式的主要作用。
循环不变式通常由三个部分组成:
- 初始化条件:在循环的第一次迭代之前,循环不变式必须成立。
- 保持条件:如果循环不变式在循环的某个迭代之前成立,那么它在下一个迭代之前也应该成立。
- 终止条件:在循环的最后一次迭代之后,循环不变式仍然成立,并且可以用它来证明算法的正确性。
循环不变式是一种非常有用的思想工具,可以帮助我们理解和证明循环和算法的正确性。正确地定义和使用循环不变式是设计和实现高质量算法的重要部分。
排序
排序问题的数学定义如下:
- 输入:一个包含 $n$ 个元素的序列 $a_1,a_2,\ldots,a_n$。
- 输出:输入序列的一个排列 $a_1',a_2',\ldots,a_n'$,使得 $a_1' \leq a_2' \leq \cdots \leq a_n'$。
排序算法的目标是将输入序列排列为符合输出要求的排列,即将输入序列中的元素按照升序排列,使得 $a_1' \leq a_2' \leq \cdots \leq a_n'$。如果是降序排列,则要求 $a_n' \leq a_{n-1}' \leq \cdots \leq a_1'$。
排序算法可以根据实现的方式和具体算法来分类,例如插入排序、选择排序、归并排序等。
经典排序算法的最坏情况运行时间和平均情况运行时间如下表所示:
| 排序算法 | 最坏情况运行时间 | 平均情况运行时间 |
|---|---|---|
| 冒泡排序 (Bubble Sort) | $O(n^2)$ | $O(n^2)$ |
| 选择排序 (Select Sort) | $O(n^2)$ | $O(n^2)$ |
| 插入排序 (Insertion Sort) | $\Theta(n^2)$ | $\Theta(n^2)$ |
| 归并排序 (Merge Sort) | $\Theta(n\lg n)$ | $\Theta(n\lg n)$ |
| 堆排序 (Heap Sort) | $O(n\lg n)$ | $O(n\lg n)$ |
| 快速排序 (Quick Sort) | $\Theta(n^2)$ | $\Theta(n\lg n)$ |
| 桶排序 (Bucket Sort) | $\Theta(n^2)$ | $\Theta(n+k)$ |
| 基数排序 (Radix Sort) | $\Theta(d(n+k))$ | $\Theta(d(n+k))$ |
其中,$n$表示输入数据的规模,$k$表示桶的个数,$d$表示数字的位数。
需要注意的是,排序算法的运行时间会受到多种因素的影响,比如输入数据的特性、算法的实现细节等,因此上述时间复杂度只是一个粗略的估计,实际情况可能会有所不同。
插入排序
算法的思路
插入排序(Insertion Sort)是一种简单直观的排序算法,它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序算法的步骤如下:
- 从第一个元素开始,该元素可以认为已经被排序。
- 取出下一个元素,在已经排序的元素序列中从后向前扫描。
- 如果该元素(已排序)大于新元素,将该元素移到下一位置。
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置。
- 将新元素插入到该位置后。
- 重复步骤2~5。
INSERTION-SORT(A)
for j = 2 to A.length
key = A[j]
// Insert A[j] into the sorted sequence A[1..j-1]
i = j - 1
while i > 0 and A[i] > key
A[i + 1] = A[i]
i = i - 1
A[i + 1] = key其中,A为待排序的数组,A.length为数组的长度。算法首先将第二个元素A[2]作为关键字key,然后将其插入到已排序的子数组A[1..j-1]中。算法通过将当前元素与已排序的子数组中的元素逐一比较,找到关键字key在已排序子数组中的位置,然后将关键字key插入到该位置。这个过程不断进行,直到将整个数组排序完毕。

在这个动画中,初始状态的数组是[5, 2, 4, 6, 1, 3]。在排序的过程中,数字从未排序的序列中一个一个被插入到已排序的序列中。在每一次迭代中,当前数字和前面的数字逐一比较,直到找到它应该插入的位置。
在第一次迭代中,数字2被插入到数字5之前,然后数组变成了[2, 5, 4, 6, 1, 3]。在第二次迭代中,数字4被插入到数字5和数字2之间,数组变成了[2, 4, 5, 6, 1, 3]。以此类推,直到整个数组被排序为止。
这个动画展示了插入排序的工作原理:在每一次迭代中,将一个未排序的元素插入到已排序的序列中,并保持已排序的序列始终有序。
使用循环不变式证明插入排序的正确性
循环不变式的描述:
- 对于数组 $A$ 中的前 $i$ 个元素,它们是已经排好序的,即 $A[1 \dots i]$ 是有序的。
证明插入排序的三个性质满足循环不变式:
- 初始化:在第一次循环开始时,数组 $A$ 的第一个元素是已排序的,因此循环不变式成立。
- 保持:假设循环不变式在第 $k$ 次迭代之前成立,即 $A[1 \dots k]$ 是有序的。在第 $k+1$ 次迭代时,我们将 $A[k+1]$ 插入到已排序的子数组 $A[1 \dots k]$ 中,以保持 $A[1 \dots k+1]$ 的有序性。具体地,我们将 $A[k+1]$ 与 $A[i]$ 依次比较,直到找到 $A[i] \leq A[k+1]$ 的位置 $j$,然后将 $A[k+1]$ 插入到位置 $j$。这样,在第 $k+1$ 次迭代之后,$A[1 \dots k+1]$ 是有序的,即循环不变式成立。
- 终止:当循环结束时,$i=n$,即整个数组都已排序。由于循环不变式在每次迭代之前都成立,因此最终循环不变式仍然成立。
因此,根据循环不变式的证明,我们可以证明插入排序的正确性。
时间复杂度分析
若数组已经排好序,最好时间复杂度: $T(n) = an+b$
若数组已经逆向排序,最坏时间复杂度: $T(n) = an^2 + bn + c$
插入排序的最好情况时间复杂度为 $O(n)$,最坏情况和平均情况时间复杂度均为 $O(n^2)$,其中 $n$ 是待排序数组的长度。
在最好情况下,待排序数组已经是有序的,每次比较只需要一次就可以找到插入位置,不需要移动任何元素,所以时间复杂度为 $O(n)$。
在最坏情况下,待排序数组是逆序的,需要比较 $1+2+\cdots+(n-1) = \frac{n(n-1)}{2}$ 次,时间复杂度为 $O(n^2)$。
在平均情况下,我们假设每个元素随机等概率地出现在任何一个位置上,那么在插入第 $i$ 个元素时,需要比较 $i/2$ 次,输入规模也是一个二次函数,时间复杂度为 $O(n^2)$。
算法的实现
fun insertionSort(array: IntArray) {
val n = array.size
for (i in 1 until n) {
val key = array[i]
var j = i - 1
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j]
j--
}
array[j + 1] = key
}
}fun insertionSort(array: IntArray) {
// 如果只有一个元素,认为已经排序好,不需要再排序了
if (array.size <= 1) {
return
}
// 从第二个元素开始,第一个元素可以认为已经排序好了
// 要执行n-1次
for (i in 1 until array.size) {
// key作为待排序元素,需要找到合适的位置插入
val key = array[i]
// 从已经排序好的元素倒序遍历,寻找可插入的位置。如果大于待排序元素,则后移,空出j这个位置
var j = i - 1
// 逐个对比i-1 .. 0区间的元素,如果元素大于待排序元素,则后移
while (j >= 0 && array[j] > key) {
array[j + 1] = array[j]
j--
}
// 将待排序字段放入到合适的位置
array[j + 1] = key
}
}归并排序
算法的思路
归并排序算法完全遵循分治策略。
- 直观上其操作如下:
- 分解:分解待排序的n个元素的序列成各具n/2个元素的两个子序列。
- 解决:使用归并排序递归地排序两个子序列。
- 合并:合并两个已排序的子序列以产生已排序的结果。
当待排序的序列长度为1时,递归“开始回升“,在这种情况下不要做任何工作,因为长度为1的每个序列都巳排好序。归并排序算法的关键操作是“合并“步骤中两个已排序序列的合并。
MERGE-SORT(A, p, r)
1 if p < r
2 q = floor((p + r) / 2)
3 MERGE-SORT(A, p, q)
4 MERGE-SORT(A, q+1, r)
5 MERGE(A, p, q, r)归并排序中的MERGE算法是将两个有序序列合并成一个有序序列的过程。
具体步骤如下:
- 1.创建一个临时数组,作为合并后的有序序列。
- 2.将左边有序序列和右边有序序列的首个元素进行比较,将较小的元素放入临时数组中,并将指向该元素的指针向后移动一个位置。
- 3.重复步骤2,直到其中一个有序序列已经全部放入临时数组中。
- 4.将未放完的有序序列中的剩余元素全部放入临时数组中。
- 5.将临时数组中的有序序列拷贝回原数组中。
注意:在实现过程中,需要考虑一些细节问题,比如边界条件的处理、两个有序序列中元素大小相同的处理方式等等。
使用哨兵的伪代码:
MERGE(A, p, q, r)
1 n1 = q - p + 1
2 n2 = r - q
3 let L[1..n1+1] and R[1..n2+1] be new arrays
4 for i = 1 to n1
5 L[i] = A[p + i - 1]
6 for j = 1 to n2
7 R[j] = A[q + j]
8 L[n1 + 1] = infinity
9 R[n2 + 1] = infinity
10 i = 1
11 j = 1
12 for k = p to r
13 if L[i] <= R[j]
14 A[k] = L[i]
15 i = i + 1
16 else
17 A[k] = R[j]
18 j = j + 1过程MERGE的详细工作过程如下:
- 第1行计算子数组A[p.. q]的长度n1
- 第2行计算子数组A[q+l.. r]的长度n2。
- 在第3行,我们创建长度分别为n1+1和n2+1的数组L和R("左”和“右")'每个数组中额外的位置将保存哨兵。
- 第4~5行的for循环将子数组A[p.. q]复制到L[1..n1], 第6~7行的for循环将子数组A[q+1..r]复制到R[1..n2]。
- 第8~9行将哨兵放在数组L和R的末尾。
- 第10~17行,通过维待以下循环不变式,执行r-p+1个基本步骤:
- 在开始第12~18行for循环的每次迭代时,子数组A[p.. k-1]按从小到大的顺序包含L[1..n1 +1]和R[1..n2 + 1]中的k-p个最小元素。进而,L[i]和R[j]是各自所在数组中未被复制回数组A的最小元素。
不使用哨兵的伪代码
MERGE(A, p, q, r)
1 nL = q – p + 1 // length of A[p : q]
2 nR = r – q // length of A[q + 1 : r]
3 let L[0 : nL – 1] and R[0 : nR – 1] be new arrays
4 for i = 0 to nL – 1 // copy A[p : q] into L[0 : nL – 1]
5 L[i] = A[p + i]
6 for j = 0 to nR – 1 // copy A[q + 1 : r] into R[0 : nR – 1]
7 R[j] = A[q + j + 1]
8 i = 0 // i indexes the smallest remaining element in L
9 j = 0 // j indexes the smallest remaining element in R
10 k = p // k indexes the location in A to fill
11 // As long as each of the arrays L and R contains an unmerged element, copy the smallest unmerged element back into A[p : r].
12 while i < nL and j < nR
13 if L[i] ≤ R[j]
14 A[k] = L[i]
15 i = i + 1
16 else
17 A[k] = R[j]
18 j = j + 1
19 k = k + 1
20 // Having gone through one of L and R entirely, copy the remainder of the other to the end of A[p : r].
21 while i < nL
22 A[k] = L[i]
23 i = i + 1
24 k = k + 1
25 while j < nR
26 A[k] = R[j]
27 j = j + 1
28 k = k + 1- https://visualgo.net/en/sorting
- https://www.cs.usfca.edu/~galles/visualization/ComparisonSort
时间复杂度分析
方式一
当一个算法包含对其自身的递归调用时,我们往往可以用递归方程或递归式来描述其运行时间,该方程根据在较小输入上的运行时间来描述在规模为n的问题上的总运行时间。然后,我们可以使用数学工具来求解该递归式并给出算法性能的界。
分治算法运行时间的递归式来自基本模式的三个步骤。
- 我们假设$T(n)$是规模为$n$的一个问题的运行时间。
- 当有$n = 1$个元素时:
- 问题规模足够小,如对某个常量$c,n <= c$, 则直接求解需要常量时间,我们将其写作$\Theta(1)$。
- 当有$n > 1$个元素时:
- 分解:如果分解问题成子问题需要时间$D(n)$
- 解决:假设把原问题分解成$a$个子问题,每个子问题的规模是原问题的$1/b$。为了求解一个规模为$n/b$的子问题,需要$T(n/b)$的时间,所以需要$aT(n/b)$的时间来求解$a$个子问题。(对归并排序,a和b都为2,然而,我们将看到在许多分治算法中,$a != b$。)
- 合并:合并子问题的解成原问题的解需要时间$C(n)$
- 当有$n = 1$个元素时:
- 那么得到递归式: $$ T\left(n\right) = \left{\begin{matrix} \Theta \left(1\right) & 若n <= c \ aT\left(n/ 2\right) + D\left(n\right) + C\left(n\right) & 其他 \ \end{matrix}\right. $$
下面我们分析建立归并排序n个数的最坏情况运行时间$T(n)$的递归式。
- 当有$n = 1$个元素时,归并排序一个元素需要常量时间。
- 当有$n > 1$个元素时,我们分解运行时间如下:
- 分解:分解步骤仅仅计算子数组的中间位置,需要常量时间,因此,$D(n) = \Theta(1)$。
- 解决:我们递归地求解2个规模均为$n/2$的子问题,将贡献$2T(n/2)$的运行时间。
- 合井:我们已经注意到在一个具有$n$个元素的子数组上过程MERGE需要$\Theta(n)$的时间,所以$C(n) = \Theta(n)$。
- 当为了分析归并排序而把函数$D(n)$与$C(n)$相加时,我们是在把一个$\Theta(n)$函数与另一个$\Theta(1)$函数相加。相加的和是n的一个线性函数,即$\Theta(n)$。
给出归并排序的最坏情况运行时间T(n)的递归式:
$$ T\left(n\right) = \left{\begin{matrix} \Theta \left(1\right) & 若n = 1 \ 2T\left(n/ 2\right) + \Theta \left(n\right) & 若n >= 1 \ \end{matrix}\right. $$
T(n)为$\Theta(n \lg n)$,其中$lg n$代表$\log _{2}n$。
因为对数函数比任何线性函数增长要慢,所以对足够大的输入,在最坏情况下,运行时间为$\Theta(n \lg n)$的归并排序将优于运行时间为$\Theta(2^{n})$的插入排序。
方式二
归并排序的时间复杂度分析主要分为两部分:分治过程和归并过程。
分治过程的时间复杂度分析:
归并排序的分治过程是一个递归过程,每次递归将原问题分成两个规模大致相同的子问题,并对这两个子问题进行递归处理。递归到最小子问题时,问题的规模为1,可以直接返回结果。因此,递归的深度为$\lg n$。每一层的时间复杂度都是$O(n)$,因为要将n个元素分成两部分,所以时间复杂度为$O(n \lg n)$。
归并过程的时间复杂度分析:
归并过程的时间复杂度与待排序序列的初始状态有关。如果待排序序列已经是有序的,则归并过程只需要比较每个元素一次就可以了,时间复杂度为$O(n)$。如果待排序序列是随机的,则每个元素在归并过程中的比较次数不会超过$\log n$次,因为每次比较都可以将问题规模缩小一半。因此,归并过程的时间复杂度为$O(n \lg n)$。
综合分治过程和归并过程的时间复杂度,归并排序的时间复杂度为$O(n \lg n)$。
算法的实现
使用哨兵的实现
fun mergeSort(arr: IntArray, p: Int, r: Int) {
if (p < r) {
val q = (p + r) / 2
mergeSort(arr, p, q)
mergeSort(arr, q + 1, r)
merge(arr, p, q, r)
}
}
fun merge(arr: IntArray, p: Int, q: Int, r: Int) {
val n1 = q - p + 1
val n2 = r - q
val left = IntArray(n1 + 1)
val right = IntArray(n2 + 1)
for (i in 0 until n1) {
left[i] = arr[p + i]
}
for (j in 0 until n2) {
right[j] = arr[q + j + 1]
}
left[n1] = Int.MAX_VALUE
right[n2] = Int.MAX_VALUE
var i = 0
var j = 0
for (k in p..r) {
if (left[i] <= right[j]) {
arr[k] = left[i]
i++
} else {
arr[k] = right[j]
j++
}
}
}这里的 mergeSort 函数接收一个整数数组,一个开始下标 p 和一个结束下标 r,表示对数组中下标从 p 到 r 的元素进行排序。首先它会判断 p 是否小于 r,如果不是,则直接返回;否则,将当前数组范围一分为二,分别递归调用 mergeSort 函数进行排序,最后再将两个已排序的子数组合并起来。
merge 函数则是用来将两个已排序的子数组合并成一个有序的数组。它接收一个整数数组 arr、两个整数下标 p 和 q,以及一个整数下标 r。首先计算出两个子数组的长度 n1 和 n2,然后创建两个新数组 left 和 right,分别用来存储子数组。接着将子数组中的元素复制到这两个新数组中。为了方便处理边界情况,我们在每个新数组的末尾都添加一个值为正无穷大的元素,这样在处理新数组时就不用每次都进行数组下标越界的判断。最后使用指针 i 和 j 分别指向两个新数组的起始位置,比较 left[i] 和 right[j] 的大小,将较小值存入数组 arr 中,并将指向该元素的指针向后移动。当 left 或 right 的所有元素都被存入 arr 中时,merge 函数的任务也就完成了。
不使用哨兵的实现
fun merge(left: IntArray, right: IntArray): IntArray {
val result = IntArray(left.size + right.size)
var i = 0
var j = 0
var k = 0
while (i < left.size && j < right.size) {
if (left[i] <= right[j]) {
result[k] = left[i]
i++
} else {
result[k] = right[j]
j++
}
k++
}
while (i < left.size) {
result[k] = left[i]
i++
k++
}
while (j < right.size) {
result[k] = right[j]
j++
k++
}
return result
}
fun mergeSort(arr: IntArray): IntArray {
if (arr.size <= 1) {
return arr
}
val mid = arr.size / 2
val left = arr.copyOfRange(0, mid)
val right = arr.copyOfRange(mid, arr.size)
val sortedLeft = mergeSort(left)
val sortedRight = mergeSort(right)
return merge(sortedLeft, sortedRight)
}这个实现中,merge 函数没有使用哨兵,而是使用了两个 while 循环来处理剩余元素。同时,mergeSort 函数调用了 Kotlin 的 copyOfRange 函数来创建子数组。
堆排序
算法的思路
堆的定义
堆排序是一种基于比较的排序算法,使用了一种数据结构——堆,它可以在$O(n\lg n)$的时间复杂度内将$n$个元素进行原址排序。堆排序的时间复杂度为$O(n\lg n)$,空间复杂度为$O(1)$,是一种不稳定的排序算法。
堆是一种完全二叉树结构,它可以分为两种:最大堆和最小堆。
- 最大堆:$A[PARENT(i)] >= A[i]$
- 最小堆:$A[PARENT(i)] <= A[i]$
- 在最大堆中,父节点的值总是大于或等于其子节点的值,而在最小堆中则相反。
堆可以使用数组来表示,具体来说,堆中的每个节点都存储在数组的一个位置上,而其子节点则存储在它的左右儿子位置上。对于下标为$i$的节点,其左儿子的下标为$2i$,右儿子的下标为$2i+1$,其父节点的下标为$\lfloor i/2 \rfloor$。
堆的高度:堆的高度取决于它所包含的节点数。对于一个有$n$个节点的堆,其高度$h$为$\lfloor \lg n \rfloor$。
堆排序的基本思想是:首先将待排序的序列构造成一个最大堆,然后将堆顶元素和序列末尾的元素进行交换,此时最大元素已经被放在了序列的末尾,接着将剩余的元素再构造成一个最大堆,重复上述操作,直到所有元素都被排序。
堆的性质:当用数组表示存储n个元素的堆时,叶结点下标分别是$\left \lfloor n/2 \right \rfloor + 1, \left \lfloor n/2 \right \rfloor + 2, ... , n$。
具体地,堆排序算法可以分为两个步骤:
- 建堆(Heapify):将待排序数组构建成一个大根堆或小根堆。以构建大根堆为例,从最后一个非叶子节点开始向前遍历,将每一个节点与它的左右子节点进行比较并交换,直到整个数组成为一个大根堆为止。
- 排序:将堆顶元素与堆的最后一个元素交换,堆的大小减一并对堆进行调整,重复这个过程直到堆的大小为1,即完成排序。
堆排序的基本过程:
- MAX-HEAPIFY:其时间复杂度为$O(\lg n)$,它是维护最大堆性质的关键。
- BUILD-MAX-HEAP:具有线性时间复杂度,功能是从无序的输入数据数组中构造一个最大堆。
- HEAPSORT:其时间复杂度为$O(n\lg n)$,功能是对一个数组进行原址排序。
堆排序的动画示意:
- 这个动画演示了如何使用最大堆对一个数组进行排序。首先,我们需要把数组构建成一个最大堆,然后每次取出最大堆中的堆顶元素,将其放到已排序的数组中,并移除最大堆中的堆顶元素,再通过 MAX-HEAPIFY 操作维护最大堆的性质,重复这个过程直到最大堆中的元素全部取出,就完成了堆排序。
- https://visualgo.net/zh/sorting
- https://www.cs.usfca.edu/~galles/visualization
- https://www.cs.usfca.edu/~galles/visualization/HeapSort.html
维护堆的性质
MAX-HEAPIFY(A, i)是用于维护最大堆性质的重要过程。它的输入为一个数组A和一个下标i。在调用MAX-HEAPIFY的时候,我们假定根结点为LEFT(i)和RIGHT(i)的二叉树都是最大堆,但这时A[i]有可能小于其孩子,这样就违背了最大堆的性质。MAX-HEAPIFY通过A[i]的值在最大堆中“逐级下降“,从而使得以下标i为根结点的子树重新遵循最大堆的性质。
MAX-HEAPIFY(A, i)
1 l = LEFT(i)
2 r = RIGHT(i)
3 if l ≤ A.heap-size and A[l] > A[i]
4 then largest = l
5 else largest = i
6 if r ≤ A.heap-size and A[r] > A[largest]
7 then largest = r
8 if largest ≠ i
9 then exchange A[i] with A[largest]
10 MAX-HEAPIFY(A, largest)时间复杂度分析
ChatGPT - 对于一个树高为h的结点来说,MAX-HEAPIFY的时间复杂度是多少?
对于一个树高为h的结点,其路径的长度为$O(h)$,每个结点的处理时间是$O(1)$,所以MAX-HEAPIFY的时间复杂度为$O(h)$。在最坏情况下,树高为$O(\lg n)$,所以在最坏情况下,MAX-HEAPIFY的时间复杂度为$O(\lg n)$。
ChatGPT - 给出MAX-HEAPIFY的时间复杂度分析
MAX-HEAPIFY的时间复杂度为$O(\lg n)$,其中$n$是堆中元素的个数。
可以使用主定理(Master Theorem)来分析MAX-HEAPIFY的时间复杂度。主定理适用于以下形式的递归式:
$$T(n) = aT(n/b) + f(n)$$
其中$a \geq 1$,$b > 1$是常数,$f(n)$是渐进正函数。
对于MAX-HEAPIFY的伪代码,可以将MAX-HEAPIFY视为对一个子树进行修复,该子树的大小为$n$,因此递归式可以表示为:
$$T(n) <= T(2n/3) + \Theta(1)$$
这里我们将$a=1$,$b=3/2$,$f(n)=\Theta(1)$。根据主定理的第二种情形,递归式的解为:
$$T(n) = O(\lg n)$$
因此,MAX-HEAPIFY的时间复杂度为$O(\lg n)$。
建堆
我们可以用自底向上的方法利用过程MAX-HEAPIFY把一个大小为n=A.length的数组A[1..n]转换为最大堆。子数组$A(\left \lfloor n/2 \right \rfloor) + 1..n)$中的元素都是树的叶结点。每个叶结点都可以看成只包含一个元素的堆。过程BUILD-MAX-HEAP对树中的其他结点都调用一次MAX-HEAPIFY
BUILD-MAX-HEAP(A)
1 A.heap-size = length[A]
2 for i = floor(A.length/2) downto 1
3 MAX-HEAPIFY(A, i)时间复杂度分析
BUILD-MAX-HEAP可以在线性时间内,把一个无序数组构造成为一个最大堆,时间复杂度:$O(n)$
堆排序算法
HEAPSORT(A)
1 BUILD-MAX-HEAP(A)
2 for i = A.length downto 2
3 exchange A[1] with A[i]
4 A.heap-size = A.heap-size - 1
5 MAX-HEAPIFY(A, 1)BUILD-MAX-HEAP 过程建立最大堆,MAX-HEAPIFY 维护最大堆性质,A.heap-size 表示当前堆的大小,exchange A[i] with A[j] 表示交换 A[i] 和 A[j] 的值。
时间复杂度分析
HEAPSORT过程的时间复杂度是$O(n \lg n)$,因为每次调用BUILD-MAX-HEAP的时间复杂度是$O(n)$,而n—1次调用MAX-HEAPIFY,每次的时间为$O(\lg n)$。
算法的实现
Kotlin代码实现
fun heapSort(array: IntArray) {
// 构建最大堆
buildMaxHeap(array)
// 从最后一个元素开始,与根节点交换并重新调整堆,重复此操作
for (i in array.size - 1 downTo 1) {
swap(array, 0, i)
maxHeapify(array, 0, i)
}
}
fun buildMaxHeap(array: IntArray) {
// 从最后一个非叶子节点开始,依次向上调整每个子堆
for (i in array.size / 2 - 1 downTo 0) {
maxHeapify(array, i, array.size)
}
}
fun maxHeapify(array: IntArray, i: Int, heapSize: Int) {
val left = 2 * i + 1 // 左子节点的下标
val right = 2 * i + 2 // 右子节点的下标
var largest = i // 最大值下标
// 与左子节点比较
if (left < heapSize && array[left] > array[largest]) {
largest = left
}
// 与右子节点比较
if (right < heapSize && array[right] > array[largest]) {
largest = right
}
// 如果最大值下标不是父节点,交换父子节点的值并递归调整子堆
if (largest != i) {
swap(array, i, largest)
maxHeapify(array, largest, heapSize)
}
}
fun swap(array: IntArray, i: Int, j: Int) {
val temp = array[i]
array[i] = array[j]
array[j] = temp
}该代码实现了堆排序算法,首先构建最大堆,然后从最后一个元素开始,与根节点交换并重新调整堆,重复此操作直到所有元素有序。其中,maxHeapify 方法实现了从一个父节点开始,递归调整其子堆为最大堆的过程;buildMaxHeap 方法实现了从最后一个非叶子节点开始,依次向上调整每个子堆的过程。
Rust代码实现
fn heap_sort<T: Ord>(arr: &mut [T]) {
let len = arr.len();
if len <= 1 {
return;
}
// 建立最大堆
for i in (0..len / 2).rev() {
max_heapify(arr, i, len);
}
// 取出堆顶元素并维护堆的性质
for i in (1..len).rev() {
arr.swap(0, i);
max_heapify(arr, 0, i);
}
}
fn max_heapify<T: Ord>(arr: &mut [T], i: usize, len: usize) {
let left = 2 * i + 1;
let right = 2 * i + 2;
let mut largest = i;
if left < len && arr[left] > arr[largest] {
largest = left;
}
if right < len && arr[right] > arr[largest] {
largest = right;
}
if largest != i {
arr.swap(i, largest);
max_heapify(arr, largest, len);
}
}在这段代码中,我们首先定义了一个 heap_sort 函数来进行堆排序,接受一个泛型参数 T 表示待排序的元素类型,实现了 Ord trait 来支持比较操作。该函数内部首先判断待排序的数组长度是否为 1 或更小,如果是则直接返回。接下来,我们调用 max_heapify 函数来建立最大堆。然后,我们使用一个循环来取出堆顶元素并维护堆的性质,直到整个数组排序完成。
在 max_heapify 函数中,我们接受三个参数,分别是待排序的数组、要建堆的根节点索引 i 和数组的长度 len。首先,我们计算出左右子节点的索引,然后找出 i、left 和 right 三者中的最大值。如果最大值不是当前节点 i,则交换它们的值并递归调用 max_heapify 函数以保持堆的性质。
快速排序
算法的思路
快速排序是一种常见的基于比较的排序算法,其基本思想可以从多个角度进行介绍。
- 分治思想:快速排序采用分治思想,将一个大问题划分成多个小问题,通过递归解决小问题,并将它们的解合并起来得到整体的解。在快速排序中,我们将待排序的数组分成两个子数组,其中一个子数组中的元素都比另一个子数组中的元素小,然后对这两个子数组分别递归地进行排序,最后将它们合并起来得到排序后的数组。
- 选取主元(pivot):快速排序算法的核心就是选取一个合适的主元,将数组划分成小于主元和大于主元两个子数组。选取主元的方法有多种,常见的方法有随机选取、取首、尾、中间元素的中位数等。
- 原地排序:快速排序是一种原地排序算法,它不需要额外的空间来存储排序后的数组,因此可以节省空间开销。
- 递归实现:快速排序采用递归的方式实现,这使得代码非常简洁,易于理解和实现。
- 时间复杂度:快速排序的时间复杂度为$O(nlogn)$,在大多数情况下表现优异。但在最坏情况下(如数组已经有序或者逆序),快速排序的时间复杂度会退化到$O(n^2)$。
总之,快速排序是一种高效、灵活的排序算法,它的基本思想可以从多个角度进行解释。
快速排序使用了分治思想,下面是对一个典型的子数组A[p .. r]进行快速排序的三步分治过程:
- 分解:数组A[p.. r]被划分为两个(可能为空)子数组A[p.. q-1]和A[q+1.. r],使得A[p .. q—l]中的每一个元素都小于等于A[q],而A[q]也小于等于A[q+1..r]中的每个元素。其中,计算下标q也是划分过程的一部分。
- 解决:通过递归调用快速排序,对子数组A[p.. q-1]和A[q+1..r]进行排序。
- 合井:因为子数组都是原址排序的,所以不需要合并操作:数组A[p.. r]巳经有序。
为了排序一个数组A的全部元素,初始调用是QUICKSORT(A, 1, A.length)。
算法的关键部分是PARTITION过程,它实现了对子数组A[p.. r]的原址重排。
QUICKSORT(A, p, r)
1 if p < r
2 q = PARTITION(A, p, r) // Partition the subarray around the pivot, which ends up in A[q].
3 QUICKSORT(A, p, q - 1) // recursively sort the low side
4 QUICKSORT(A, q + 1, r) // recursively sort the high side
PARTITION(A, p, r)
1 x = A[r] // the pivot
2 i = p - 1 // highest index into the low side
3 for j = p to r - 1 // process each element other than the pivot
4 if A[j] ≤ x // does this element belong on the low side
5 i = i + 1 // index of a new slot in the low side
6 exchange A[i] with A[j] // put this element there
7 exchange A[i + 1] with A[r] // pivot goes just to the right of the low side
8 return i + 1 // new index of the pivotPARTITION总是选择一个x=A[r]作为主元(pivot element) , 并围绕它来划分子数组A[p.. r]。
随着程序的执行,数组被划分成4个(可能有空的)区域。在第3~6行循环体的每一轮迭代开始时,对于任意数组下标k,有:
- 若 p <= k <= i,则 A[k] <= x。
- 若 i + 1 <= k <= j—1,则 A[k] > x。
- 若 k = r,则 A[k] = x。
- 若 j <= k <= r-1,无限制,待排序。
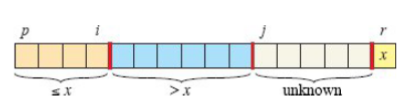
在子数组A[p.. r]上,PARTITION维护了4个区域。A[p.. i]区间内的所有值都小于等于x,A[i+1.. j-1]区间内的所有值都大于x,A[r]=x。子数组A[j.. r—1]中的值可能属于任何一种情况。
在PARTITION的最后两行中,通过将主元与最左的大于x的元素进行交换,就可以将主元移到它在数组中的正确位置上,并返回主元的新下标。
PARTITION在子数组A[p.. r]上的时间复杂度是$\Theta(n)$。

https://www.cs.usfca.edu/~galles/visualization/ComparisonSort.html
时间复杂度分析
最坏情况划分
当划分产生的两个子问题分别包含了n-1个元素和0个元素时,快速排序的最坏情况发生了。
算法运行时间的递归式可以表示为:$T(n) = T(n-1) + T(O) + \Theta(n) = T(n—1) + \Theta(n)$,解为$T(n) = \Theta(n^2)$
最好情况划分
在可能的最平衡的划分中,PARTITION得到的两个子问题的规模都不大于n/2。
在这种情况下,快速排序的性能非常好。此时,算法运行时间的递归式为:$T(n) = 2T(n/2) + \Theta(n)$ 。根据主定理(定理4.1)的情况2,上述递归式的解为$T(n)=\Theta(n \lg n)$。
通过在每一层递归中都平衡划分子数组,我们得到了一个渐近时间上更快的算法。
快速排序的最好情况是每次选择的枢纽元素都恰好将待排序数组均分为两个相等大小的子数组,即每次划分得到的两个子数组的长度均为 $n/2$。这样,快速排序的递归树的深度就为 $\Theta(\lg n)$,每层所需的时间复杂度为 $\Theta(n)$,因此总时间复杂度为 $\Theta(n\lg n)$。这种情况发生的概率非常小,但是在某些特定的数据分布下可能会出现。
平均情况划分
事实上,任何一种常数比例的划分都会产生深度为$\Theta(lg n)$的递归树,其中每一层的时间代价都是$O(n)$。因此,只要划分是常数比例的,算法的运行时间总是$O(n \lg n)$。
算法的随机化版本
与始终采用A[r]作为主元的方法不同,随机抽样是从子数组A[p .. r]中随机选择一个元素作为主元。为达到这一目的,首先将A[r]与从A[p.. r]中随机选出的一个元素交换。通过对序列p,...,r的随机抽样,我们可以保证主元元素x=A[r]是等概率地从子数组的r-p+1个元素中选取的。因为主元元素是随机选取的,我们期望在平均情况下,对输入数组的划分是比较均衡的。
对PARTITION和QUICKSORT的代码的改动非常小。在新的划分程序中,我们只是在真正进行划分前进行一次交换:
RANDOMIZED-QUICKSORT(A, p, r)
1 if p < r
2 q = RANDOMIZED-PARTITION(A, p, r)
3 RANDOMIZED-QUICKSORT(A, p, q − 1)
4 RANDOMIZED-QUICKSORT(A, q + 1, r)
RANDOMIZED-PARTITION(A, p, r)
1 i = RANDOM(p, r)
2 exchange A[r] with A[i]
3 return PARTITION(A, p, r)为什么我们分析随机化算法的期望运行时间,而不是其最坏运行时间呢?
分析随机化算法的期望运行时间是因为随机化算法的运行时间会受到输入数据的影响,而随机化算法的设计是为了使其在平均情况下表现良好。因此,我们需要通过概率论的方法来估算随机化算法的期望运行时间,以便更好地了解其性能和预测其运行时间。
相比之下,最坏情况下的运行时间对于确定性算法更为重要,因为它可以保证在任何情况下算法都能在这个时间内完成。但对于随机化算法而言,最坏情况下的运行时间并不能真实地反映算法的性能,因为最坏情况很少出现,而平均情况则更符合实际应用。因此,我们更关注随机化算法在平均情况下的表现,以便更好地评估其性能。
算法的实现
Kotlin代码实现
fun quickSort(arr: IntArray, p: Int, r: Int) {
if (p < r) {
val q = partition(arr, p, r)
quickSort(arr, p, q - 1)
quickSort(arr, q + 1, r)
}
}
fun partition(arr: IntArray, p: Int, r: Int): Int {
val pivot = arr[r]
var i = p - 1
for (j in p until r) {
if (arr[j] <= pivot) {
i++
swap(arr, i, j)
}
}
swap(arr, i + 1, r)
return i + 1
}
fun swap(arr: IntArray, i: Int, j: Int) {
val temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}这个算法使用了递归方法对数组进行排序。首先选择一个元素作为基准值(pivot),然后将小于等于基准值的元素放到数组左边,将大于基准值的元素放到数组右边,然后递归地对左右两个子数组进行排序,直到整个数组有序。
Kotlin代码实现-随机化版本
fun quicksortRandomized(A: IntArray, p: Int, r: Int) {
if (p < r) {
val q = randomizedPartition(A, p, r)
quicksortRandomized(A, p, q - 1)
quicksortRandomized(A, q + 1, r)
}
}
fun randomizedPartition(A: IntArray, p: Int, r: Int): Int {
val i = (p..r).random()
A[r] = A[i].also { A[i] = A[r] }
return partition(A, p, r)
}
fun partition(A: IntArray, p: Int, r: Int): Int {
val x = A[r]
var i = p - 1
for (j in p until r) {
if (A[j] <= x) {
i++
A[i] = A[j].also { A[j] = A[i] }
}
}
A[i + 1] = A[r].also { A[r] = A[i + 1] }
return i + 1
}其中,quicksortRandomized 函数是随机化快速排序的入口函数,它接受待排序数组 A、排序区间的左右边界 p 和 r 作为输入。randomizedPartition 函数会随机选取一个元素作为主元,并把它与区间末尾的元素交换位置,然后调用 partition 函数对区间进行划分。partition 函数按照主元的大小把数组划分成两个子区间,然后返回主元的位置。
在 randomizedPartition 函数中,我们使用 kotlin.random 库的 random() 函数随机生成一个下标 i,并将位置 i 的元素与区间末尾的元素交换位置,然后再调用 partition 函数。这样可以避免选择恶意输入时,快速排序的时间复杂度退化到最坏情况。
你可以像下面这样调用 quicksortRandomized 函数进行排序:
val array = intArrayOf(5, 2, 4, 6, 1, 3)
quicksortRandomized(array, 0, array.size - 1)
println(array.contentToString()) // 输出 [1, 2, 3, 4, 5, 6]冒泡排序
算法的思路
冒泡排序是一种简单的排序算法,其基本思想是通过不断交换相邻的元素,将最大的元素逐渐“冒泡”到最后面。具体来说,算法从数组的第一个元素开始,比较相邻的两个元素,如果前一个元素比后一个元素大,就交换它们的位置,这样一趟过去后,最大的元素就“冒泡”到了数组的末尾。然后算法继续对剩余的元素进行相同的操作,直到整个数组都有序。
冒泡排序的过程可以用以下几个步骤来描述:
- 从数组的第一个元素开始,依次比较相邻的两个元素。
- 如果前一个元素比后一个元素大,就交换它们的位置。
- 重复步骤1和步骤2,直到整个数组都有序。在每一趟排序中,都会将当前未排序部分的最大元素“冒泡”到最后。
- 如果在某一趟排序中没有发生交换,则说明数组已经有序,可以提前结束排序。
升序版本的伪代码:
BubbleSort(A)
1 for i = 1 to A.length - 1
2 for j = 1 to A.length - i - 1
3 if A[j] > A[j+1]
4 exchange A[j] with A[j+1]降序版本的伪代码:
BubbleSort(A)
1 for i = 1 to A.length - 1
2 for j = A.length downto i + 1
3 if A[j] < A[j-1]
4 exchange A[j] with A[j-1]其中,A 为待排序的数组,A.length 表示数组的长度。算法从数组的第一个元素开始,比较相邻的元素并交换,一直到最后一个元素,每一轮比较将最大的元素“冒泡”到最后,然后再次从数组的第一个元素开始比较,直到没有任何一对元素需要交换为止。
- https://visualgo.net/bn/sorting
冒泡排序的时间复杂度
由于每一趟排序都会将一个未排序部分的最大元素“冒泡”到最后,所以算法的时间复杂度为$O(n^2)$。
此外,由于算法的操作只涉及相邻元素之间的比较和交换,所以空间复杂度为$O(1)$。
算法的实现
Kotlin代码实现
fun bubbleSort(array: IntArray) {
val n = array.size
for (i in 0 until n - 1) {
for (j in 0 until n - i - 1) {
if (array[j] > array[j + 1]) {
val temp = array[j]
array[j] = array[j + 1]
array[j + 1] = temp
}
}
}
}这个实现使用两层循环,外层循环控制冒泡排序的次数,内层循环对每一次冒泡进行比较并交换。在每一次内层循环结束后,未排序的部分中最大的元素会被放在数组的最后面。时间复杂度为 $O(n^2)$。
选择排序
算法的思路
选择排序的基本思路是:每次从未排序部分选出最小(大)的元素,放到已排序部分的末尾,重复该操作直到所有元素都排好序。
具体来说,选择排序可以按以下步骤进行:
- 遍历整个数组,找到最小(大)的元素。
- 将该元素与数组的第一个元素交换位置。
- 接着从第二个元素开始遍历,再次找到未排序部分的最小(大)元素,将其与数组的第二个元素交换位置。
- 重复上述操作,直到数组完全有序。
因为每次只选择未排序部分的最小(大)元素,所以选择排序的时间复杂度为 O(n^2)。虽然选择排序的时间复杂度较高,但它的实现简单,所以在一些特殊场景下,比如数据规模较小时,选择排序还是有一定实用价值的。
Selection-Sort(A)
1. for i = 1 to A.length - 1
2. min_index = i
3. for j = i + 1 to A.length
4. if A[j] < A[min_index]
5. min_index = j
6. swap A[i] with A[min_index]时间复杂度
选择排序的时间复杂度是$O(n^2)$,其中n是待排序数组的长度。其主要原因是因为在每一次循环中,都要比较未排序部分的所有元素,找到最小的元素并进行交换,因此需要进行n-1次循环,每次循环都要比较n-i次,其中i是当前已经排序的元素个数。因此总的比较次数是n*(n-1)/2,即$O(n^2)$。
在最好情况下,也需要进行n-1次循环,因此时间复杂度也是$O(n^2)$。在最坏情况下,同样需要进行n-1次循环,但是每次循环都需要进行n-i次比较,因此时间复杂度也是O(n^2)。因此,无论输入数据的顺序如何,选择排序的时间复杂度都是$O(n^2)$。
Kotlin代码实现
fun selectionSort(arr: IntArray) {
val n = arr.size
for (i in 0 until n - 1) {
var minIndex = i
for (j in i + 1 until n) {
if (arr[j] < arr[minIndex]) {
minIndex = j
}
}
if (minIndex != i) {
val temp = arr[i]
arr[i] = arr[minIndex]
arr[minIndex] = temp
}
}
}这个实现中,我们首先得到数组的长度 n,然后进行外部循环,从第一个元素到倒数第二个元素遍历数组。在每次外部循环中,我们都会先将当前元素下标 i 赋值给 minIndex,然后再进行内部循环。内部循环从 i+1 开始遍历数组,找到最小元素的下标并将其赋值给 minIndex。如果 minIndex 不等于 i,那么就交换 arr[i] 和 arr[minIndex]。
在外部循环结束后,数组就被排好序了。这个算法的时间复杂度为 $O(n^2)$,与冒泡排序和插入排序相同,但是由于选择排序每次交换的次数比较少,所以通常比冒泡排序和插入排序的性能要好。
计数排序
算法的思想
计数排序假设n个输入元素中的每一个都是在0到k区间内的一个整数,其中k为某个整 数。当 k=$O(n)$ 时,排序的运行时间为 $\Theta(n)$
计数排序的基本思想是:对每一个输入元素 x, 确定小于x的元素个数。利用这一信息,就可以直接把x放到它在输出数组中的位置上了。例如,如果有 17 个元素小于x, 则x就应该在 第18个输出位置上。当有几个元素相同时,这一方案要略做修改。因为不能把它们放在同一个输出位置上。
在计数排序算法的代码中,假设输入是一个数组 A[1.. n], A. length=n。我们还需要两个数组:B[1.. n]存放排序的输出,C[0.. k]提供临时存储空间。
COUNTING-SORT(A, n, k)
1 let B[1 : n] and C [0 : k] be new arrays
2 for i = 0 to k
3 C[i] = 0
4 for j = 1 to n
5 C[A[j]] = C[A[j]] + 1
6 // C[i] now contains the number of elements equal to i.
7 for i = 1 to k
8 C[i] = C[i] + C[i – 1]
9 // C[i] now contains the number of elements less than or equal to i.
10 // Copy A to B, starting from the end of A.
11 for j = n downto 1
12 B[C[A[j]]] = A[j]
13 C[A[j]] = C[A[j]] – 1 // to handle duplicate values
14 return B- https://www.cs.usfca.edu/~galles/visualization/CountingSort.html
在第2~3行for循环的初始化操作之后,数组C的值全被置为0;
在第4~5行的for循环遍历每一个输入元素。如果一个输入元素的值为i,就将C[i]值加1。于是,在第5行执行完后,C[i]中保存的就是等于i的元素的个数,其中i=0,1, ..., k。
在第7~8行通过加总计算确定对每一个i=0,1, ..., k, 有多少输入元素是小于或等于i的。
在第10~12行的for循环部分,把每个元素A[j]放到它在输出数组B中的正确位置上。如果所有n个元素都是互异的,那么当第一次执行第10行时,对每一个A[j]值来说,C[A[j]]就是A[j]在输出数组中的最终正确位置。这是因为共有C[A[j]]个元素小于或等于A[j]。因为所有的元素可能并不都是互异的,所以,我们每将一个值A[j]放入数组B中以后,都要将C[A[j]]的值减1。这样,当遇到下一个值等于A[j]的输入元素(如果存在)时,该元素可以直接被放到输出数组中A[j]的前一个位置上。
时间复杂度分析
第2~3行的for循环所花时间为$\Theta(k)$,第4~5行的for循环所花时间为$\Theta(n)$,第7~8行的for循环所花时间为$\Theta(k)$,第10~12行的for循环所花时间为$\Theta(n)$。总的时间代价就是$\Theta(k+n)$。在实际工作中,当k=$O(n)$时,我们一般会采用计数排序,这时的运行时间为$\Theta(n)$。
计数排序的一个重要性质就是它是稳定的:具有相同值的元素在输出数组中的相对次序与它们在输入数组中的相对次序相同。也就是说,对两个相同的数来说,在输入数组中先出现的数,在输出数组中也位于前面。
Kotlin代码实现
fun countingSort(array: IntArray, k: Int): IntArray {
val count = IntArray(k + 1)
for (element in array) {
count[element]++
}
for (i in 1..k) {
count[i] += count[i - 1]
}
val result = IntArray(array.size)
for (i in array.size - 1 downTo 0) {
result[count[array[i]] - 1] = array[i]
count[array[i]]--
}
return result
}基数排序
算法的思想
基数排序是一种非比较排序算法,它的基本思想是将待排序的元素分割成不同的数字或字符,然后按照每个位数分别进行比较,以达到排序的目的。基数排序的工作过程如下:
- 首先,将待排序的元素按照其个位数字进行排序,形成若干个桶,每个桶内的元素的个位数相同。
- 接下来,将每个桶内的元素按照其十位数字进行排序,形成若干个桶。
- 以此类推,直到按照最高位数字排序完成。
- 最终得到的序列就是有序的。
需要注意的是,每次排序时,元素的顺序不能改变。因此,对于每一位的排序,都需要使用稳定的排序算法,如插入排序或计数排序。
RADIX-SORT(A, d)
1. for i = 1 to d do
2. use a stable sorting algorithm to sort array A on digit i时间复杂度
基数排序的时间复杂度是 $O(d(n+k))$,其中 $d$ 是元素的最大位数,$n$ 是元素的个数,$k$ 是每一位数字可能的取值数。基数排序的空间复杂度是 $O(n+k)$,其中 $k$ 是每一位数字可能的取值数。因此,当 $k$ 比较小的时候,基数排序比较适用。
Kotlin代码实现
fun radixSort(arr: IntArray) {
if (arr.size < 2) return
// 找到最大数,确定位数
var maxVal = arr[0]
for (i in 1 until arr.size) {
if (arr[i] > maxVal) {
maxVal = arr[i]
}
}
var radix = 1
while (maxVal / radix > 0) {
val count = IntArray(10) // 0 ~ 9
// 统计每个桶中的元素个数
for (i in arr) {
count[(i / radix) % 10]++
}
// 计算每个桶中最后一个元素的位置
for (i in 1 until count.size) {
count[i] += count[i - 1]
}
// 将元素按位数放入桶中
val temp = IntArray(arr.size)
for (i in arr.size - 1 downTo 0) {
temp[count[(arr[i] / radix) % 10] - 1] = arr[i]
count[(arr[i] / radix) % 10]--
}
// 将排序结果复制回原数组
for (i in arr.indices) {
arr[i] = temp[i]
}
radix *= 10
}
}桶排序
算法的思想
桶排序(bucket sort)假设输人数据服从均分布平均情况下它的时间价为$O(n)$。
与计数排序类似,因为对输入数据作了某种假设,桶排序的速度也很快。具体来说,计数排序假设输入数据都属于一个小区间内的整数,而桶排序则假设输人是由一个随机过程产生,该过程将元素均匀、独立地分布在[0,1)区间上。
桶排序将[0,1)区间划分为n个相同大小的子区间,或称为桶。然后,将n个输人数分别放到各个桶中。因为输人数据是均匀、独立地分布在[0,1)区间上,所以一般不会出现很多数落在同一个桶中的情况。为了得到输出结果,我们先对每个桶中的数进行排序,然后遍历每个桶,按照次序把各个桶中的元素列出来即可。
在桶排序的代码中,我们假设输入是一个包含n个元素的数组A,且每个元素A[i]满足0 <= A[i] < 1。此外,算法还需要一个临时数 B[0..n-1]来存放表(即桶),并假设存在一种用于维护这些链表的机制。
BUCKET-SORT(A)
1. n = length[A]
2. let B[0...n-1] be a new array
3. for i = 0 to n-1
4. make B[i] an empty list
5. for i = 1 to n
6. insert A[i] into list B[⌊n * A[i]⌋]
7. for i = 0 to n-1
8. sort list B[i] with insertion sort
9. concatenate the lists B[0], B[1], ..., B[n-1] together in order to get the sorted array- https://www.cs.usfca.edu/~galles/visualization/BucketSort.html
其中n为数组A的长度,B为桶数组,B[i]表示第i个桶,存放A中值属于桶i的元素。第5步把A中元素分配到对应的桶中,第8步用插入排序算法对每个桶中的元素进行排序,最后在第9步把所有桶中的元素按顺序合并到一起,得到排好序的数组。
时间复杂度
桶排序的时间复杂度取决于两个因素:桶的数量和桶内部排序算法的时间复杂度。
设有n个元素待排序,将它们均匀地划分到m个桶中。如果桶的数量m接近n,且每个桶内的元素个数k也接近n,那么桶排序的时间复杂度为$O(n)$。这是因为分配元素到桶中的时间复杂度为$O(n)$,在每个非空的桶中进行内部排序的时间复杂度为$O(k \lg k)$,总时间复杂度就是$O(n + m * k \lg k)$。
但是,如果桶的数量m较小,例如常数级别,那么桶排序的时间复杂度就会降低到$O(n \lg n)$。这是因为分配元素到桶中的时间复杂度为$O(n)$,在每个非空的桶中进行内部排序的时间复杂度为$O(n / m * \lg (n / m))$,总时间复杂度就是$O(n + n * \lg(n / m))$。
因此,桶排序的时间复杂度可以通过合理选择桶的数量m来优化。一般而言,当数据分布比较均匀时,选择合适的桶数量可以使得桶排序的时间复杂度明显优于其他排序算法
Kotlin代码实现
fun bucketSort(A: DoubleArray): DoubleArray {
val n = A.size
val B = Array(n) { mutableListOf<Double>() }
val C = DoubleArray(n)
for (i in 0 until n) {
// 每个元素A[i]满足0 <= A[i] < 1
B[(n * A[i]).toInt()].add(A[i])
}
for (i in 0 until n) {
insertionSort(B[i])
}
var index = 0
for (i in 0 until n) {
for (j in B[i].indices) {
C[index++] = B[i][j]
}
}
return C
}
fun insertionSort(A: MutableList<Double>) {
for (j in 1 until A.size) {
val key = A[j]
var i = j - 1
while (i >= 0 && A[i] > key) {
A[i + 1] = A[i]
i--
}
A[i + 1] = key
}
}其中,A是待排序的数组,B是存放元素的桶,C是存放排序后元素的数组。函数insertionSort是用来对桶中元素进行插入排序的。
期望为线性时间的选择算法
算法的思想
RANOOMIZED-SELECT算法是以快速排序算法为模型的。与快速排序一样,我们仍然将输入数组进行递归划分。但与快速排序不同的是,快速排序会递归处理划分的两边,而RANOOMIZEDSELECT只处理划分的一边。这一差异会在性能分析中体现出来:快速排序的期望运行时间是团$\Theta(n \lg n)$, 而RANOOMIZED-SELECT的期望运行时间为$\Theta(n)$。这里,假设输入数据都是互异的。
RANOOMIZED-SELECT的伪代码,它返回数组A[p..r]中第i小的元素。
在这些伪代码中,A是一个数组,p是起始下标,r是结束下标,i表示要查找的元素在整个数组中的排名。RANDOMIZED-SELECT算法的作用是在A中查找第i小的元素。
RANDOMIZED-SELECT (A, p, r, i)
1 if p == r
2 return A[p]
3 q = RANDOMlZED-PARTITION(A, p, r)
4 k = q - p + 1
5 if i == k // the pivot value is the answer
6 return A[q]
7 else if i < k
8 return RANOOMIZED-SELECT(A, p, q - 1, i)
9 else
10 return RANOOMIZED-SELECT(A, q + l, r, i-k)RANDOMIZED-SELECT的运行过程如下:
- 第1行检查递归的基本情况,即A[p.. r]中只包括一个元素。在这种情况下,i必然等于1,在第2行,我们只需将A[p]返回作为第i小的元素即可。
- 第3行的RANDOMIZED-PARTITION,将数组A[p.. r]划分为两个(可能为空的)子数组A[p.. q-1]和A[q+1..r], 使得A[p.. q-1]中的每个元素都小于或等于A[q], 而A[q]小于A[q+1.. r]中的每个元素。与快速排序中一样,我们称A[q]为主元(pivot)。
- 第4行计算子数组A[p.. q]内的元素个数k,即处于划分的低区的元素的个数加1,这个1指主元。
- 第5行检查A[q]是否是第i小的元素。
- 如果是,第6行就返回A[q]。
- 否则,算法要确定第i小的元素落在两个子数组A[p.. q-1]和A[q+1..r]的哪一个之中。
- 如果i < k,则要找的元素落在划分的低区。第8行就在低区的子数组中进一步递归查找。
- 如果i > k,则要找的元素落在划分的高区中。因为我们已经知道了有K个值小于A[p.. r]中第t小的元素,即A[p.. q]内的元素,所以,我们所要找的元素必然是A[q+1..r]中的第i—k小的元素。它在第9行中被递归地查找。
其中,RANDOMIZED-PARTITION是用随机化的方法对数组进行划分的过程,其伪代码如下:
RANDOMIZED-PARTITION(A, p, r)
1 i = RANDOM(p, r)
2 exchange A[r] with A[i]
3 return PARTITION(A, p, r)PARTITION是对数组进行划分的过程,其伪代码如下:
PARTITION(A, p, r)
1 x = A[r]
2 i = p - 1
3 for j = p to r - 1
4 if A[j] <= x
5 i = i + 1
6 exchange A[i] with A[j]
7 exchange A[i + 1] with A[r]
8 return i + 1时间复杂度
在最坏情况下,该算法的时间复杂度为 $O(n^2)$,但是由于每次随机选择主元,期望时间复杂度为 $O(n)$。
Kotlin代码实现
import kotlin.random.Random
fun randomizedSelect(A: IntArray, p: Int, r: Int, i: Int): Int {
if (p == r) {
return A[p]
}
val q = randomizedPartition(A, p, r)
val k = q - p + 1
return when {
i == k -> A[q]
i < k -> randomizedSelect(A, p, q - 1, i)
else -> randomizedSelect(A, q + 1, r, i - k)
}
}
fun randomizedPartition(A: IntArray, p: Int, r: Int): Int {
val i = Random.nextInt(p, r + 1)
A[i] = A[r].also { A[r] = A[i] }
return partition(A, p, r)
}
fun partition(A: IntArray, p: Int, r: Int): Int {
val x = A[r]
var i = p - 1
for (j in p until r) {
if (A[j] <= x) {
i++
A[i] = A[j].also { A[j] = A[i] }
}
}
A[i + 1] = A[r].also { A[r] = A[i + 1] }
return i + 1
}randomizedSelect 函数实现了从数组 A 中寻找第 i 小的元素,其中 p 和 r 分别表示待寻找的数组下标范围。该函数的实现基于随机化的思想,在递归过程中对待查找区间进行分割并进行递归查找,直到找到第 i 小的元素。
randomizedPartition 函数实现了随机划分数组 A 的过程,其中随机选取下标为 $i$ 的元素,并以该元素为枢纽元素进行划分,返回枢纽元素的下标。
partition 函数实现了快速排序中常规的划分过程,其中枢纽元素选为数组的最后一个元素,将待划分区间划分为两部分,并返回枢纽元素最终所在的下标。
