算法分析

如何分析算法

何为算法分析

分析算法意味着预测算法需要的资源。

• 输入规模：

  • 依赖于研究的问题。

• 运行时间：

  • 一个算法在特定输人上的运行时间是指执行的基本操作数或步数。

• 最坏情况与平均情况分析：

  • 在进行算法分析时，我们通常关注最坏情况下的时间复杂度，因为它们可以给出算法的上界。同时，我们也可以考虑平均情况下的时间复杂度和最好情况下的时间复杂度，它们能够更好地反映算法的实际效率。

• 增长量级：

  • 我们真正感兴趣的是运行时间的增长率或增长量级。所以我们只考虑公式中最重要的项（例如，a$n^{2}$)，因为当n的值很大时，低阶项相对来说不太重要。我们也忽略最重要的项的常系数，因为对大的输入，在确定计算效率时常量因子不如增长率重要。
    • 如果一个算法的最坏情况运行时间具有比另一个算法更低的增长量级，那么我们通常认为前者比后者更有效。
    • 一个$\Theta(n^{2})$的算法在最坏情况下比另一个$\Theta(n^{3})$的算法要运行得更快。

时间复杂度分析的类型

• 最好时间复杂度
• 最坏时间复杂度
• 平均时间复杂度
• 均摊时间复杂度

ChatGPT对"分析算法的渐进复杂度的方法？"的回答

分析算法的渐进复杂度是算法设计和优化中的重要环节，常用的方法有以下几种：

• 直接计算法：对算法的每个操作进行精确计数，然后计算总的操作次数。该方法非常直观，但也很繁琐，需要对算法的每个细节进行仔细的分析，不适合用于复杂的算法。

• 估计法：该方法通常基于以下两个原则：一是算法的基本操作所需的时间是一个固定的常数，二是算法中的一些操作执行的次数与输入规模$n$成正比。通过对这两个原则进行分析，可以得出算法的渐进复杂度。在估计算法复杂度时，通常采用大O符号来表示算法的渐进复杂度，即$O(g(n))$表示算法的最坏时间复杂度为$g(n)$，$g(n)$为某个函数。

• 递归方程法：递归方程法通常适用于递归算法的分析。该方法通常基于以下原则：算法在每一层递归中执行的操作次数是一个固定的常数，而递归的深度与输入规模$n$成正比。通过列出递归方程，然后求解其解析式或递推式，可以得出算法的渐进复杂度。

• 主定理法：主定理法是一种特殊的递归方程法，适用于形如$T(n)=aT(n/b)+f(n)$的递归方程的求解。主定理法可以方便地求解许多经典的递归算法的渐进复杂度，如二分查找、归并排序等。

以上是常用的分析算法渐进复杂度的方法，不同的算法和情况可能适用不同的方法。在实际应用中，通常需要结合具体的情况选择最合适的方法进行分析。

如何理解渐进记号

我们关心当输入规模无限增加时，在极限中，算法的运行时间如何随着输入规模的变大而增加。

通常，渐近地更有效的某个算法对除了很小的输入以外的所有情况将是最好的选择。

渐进记号、函数、运行时间

• 定理3.1

  • 对任意两个函数$f(n)$和$g(n)$，我们有$f(n)=\Theta(g(n))$， 当且仅当$f(n)=O(g(n))$且$f(n)=\Omega(g(n))$

• $\Theta$ 记号

  • 定义这个记号意指什么。对一个给定的函数$g(n)$，用$\Theta(g(n))$来表示以下函数的集合：
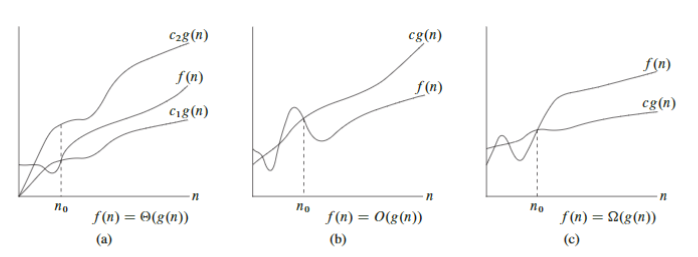
    • $\Theta(g(n))$ = { $f(n)$ : 存在正常量$c_{1}$、$c_{2}$和$n_{0}$，使得对所有$n >= n_{0}$，有 $0 <= c_{1}g(n) <= f(n) <= c_{2}g(n)$ }
    • 若存在正常量$c_{1}$和$c_{2}$，使得对于足够大的$n$，函数$f(n)$能“夹入"$c_{1}g(n)$与$c_{2}g(n)$之间，则$f(n)$属于集合$\Theta(g(n))$。
    • 因为$\Theta(g(n))$是一个集合，所以可以记"$f(n) \in \Theta(g(n))$"， 以指出$f(n)$是$\Theta(g(n))$的成员。
    • 作为替代，我们通常记"$f(n)=\Theta(g(n))$"以表达相同的概念。
    • 对所有$n >= n_{0}$，函数$f(n)$在一个常量因子内等于$g(n)$，我们称$g(n)$是$f(n)$的一个渐近紧确界(asymptotically tight bound)。
  • • $\Theta$记号渐近地给出一个函数的上界和下界。
  • 我们将经常使用记号$\Theta(1)$来意指一个常量或者关于某个变量的一个常量函数。

• $O$ 记号

  • 当只有一个渐近上界时，使用$O$记号。
  • 对于给定的函数$g(n)$，用$O(g(n))$来表示以下函数的集合：(读作“$大Og(n)$"，有时仅读作"$Og(n)$")
    • $O(g(n))$ = {$f(n)$: 存在正常量$c$和$n_{0}$， 使得对所有$n >= n_{0}$，有$0 <= f(n) <= cg(n)$}
    • 我们使用$O$记号来给出函数的一个在常量因子内的上界。
    • 我们记$f(n)=O(g(n))$以指出函数$f(n)$是集合$O(g(n))$的成员。注意，$f(n)=\Theta(g(n))$蕴涵着$f(n)=O(g(n))$， 因为$\Theta$是一个比$O$记号更强的概念。
  • 使用$O$记号，我们常常可以仅仅通过检查算法的总体结构来描述算法的运行时间。
  • 当我们说“运行时间为$O(n^2)$"时
    • 意指存在一个$O(n^2)$的函数$f(n)$，即$f(n)=O(n^2)$，使得对$n$的任意值，不管选择什么特定的规模为$n$的输入，其运行时间的上界都是$g(n)=n^2$。这也就是说最坏情况运行时间为$O(n^2)$。
    • 通常表示算法的时间复杂度上界是$n^2$，即当输入规模为$n$时，算法的最坏情况时间复杂度为$O(n^2)$。其中，$n$通常表示输入数据的规模大小。
    • 时间复杂度是用来衡量算法的效率的，它表示当输入规模增加时，算法所需的时间增长的数量级。$O(n^2)$的时间复杂度表示当输入规模增加时，算法所需的时间将按照$n^2$的数量级增长。

• $\Omega$记号

  • 正如$O$记号提供了一个函数的渐近上界，$\Omega$记号提供了渐近下界。
  • 对于给定的函数$g(n)$，用$\Omega(g(n)$来表示以下函数的集合: （读作“大$\Omega(g(n)$"，有时仅读作"$\Omega(g(n)$")
    • $\Omega(g(n))$ = {$f(n)$: 存在正常量$c$和$n_{0}$，使得对所有$n >= n_{0}$，有$0 <= cg(n) <= f(n)$}
  • 当称一个算法的运行时间为$\Omega(g(n))$时，我们意指对每个$n$值，不管选择什么特定的规模为$n$的输入，只要$n$足够大，对那个输入的运行时间至少是$g(n)$的常量倍。
  • 这是对一个算法的最好情况运行时间给出的一个下界。

• $o$ 记号

  • $O$记号提供的渐近上界可能是也可能不是渐近紧确的。界$2n^{2} = \Theta(n^{2})$是渐近紧确的，但是界$2n = \Theta(n^{2})$却不是。
  • 使用$o$记号来表示一个非渐近紧确的上界。
  • 形式化地定义$o(g(n))$ 为以下集合：
    • $o(g(n))$ = {$f(n)$ : 对任意正常量$c > 0$，存在常量$n_{0} > 0$，使得对所有$n >= n_0$，有$0 <= f(n) < cg(n)$}
  • $O$记号与$o$记号的定义类似。主要的区别是在$f(n)=O(g(n))$中，界$0 <= f(n) <= cg(n)$对某个常量$c > 0$成立，但在$f(n)=o(g(n))$中，界$0 <= f(n) < cg(n)$对所有常量$c > 0$成立。
  • 在$o$记号中，当$n$趋于无穷时，函数$f(n)$相对于$g(n)$来说变得微不足道了，即
    • $\lim \limits_{n \rightarrow ∞} \frac{f(n)}{g(n)} = 0$

• $\omega$ 记号

  • 使用$\omega$ 记号来表示一个非渐近紧确的下界。
  • $f(n) \in \omega(g(n))$ 当且仅当 $g(n) \in o(f(n))$
  • 形式化地定义$\omega(g(n)$)为以下集合:
    • $omega(g(n))$ = {$f(n)$ : 对任意正常量$c > 0$，存在常量$n_{0} > 0$，使得对所有$n >= n_0$，有$0 <= cg(n) < f(n)$}
  • 关系$f(n) \in \omega(g(n))$蕴涵着
    • $\lim \limits_{n \rightarrow ∞} \frac{f(n)}{g(n)} = ∞$

ChatGPT对"分别介绍一下，$\Theta$符号、$O$符号、$\Omega$符号的含义"的回答。

$\Theta$符号、$O$符号和$\Omega$符号都是用于描述算法的渐进复杂度的符号。

$O$符号通常用于描述算法的最坏时间复杂度，表示算法在输入规模趋近于无穷大时，其运行时间的增长速度不会超过一个固定的上界。具体来说，如果一个算法的最坏时间复杂度为$O(f(n))$，那么随着输入规模$n$的增加，算法的运行时间不会超过一个常数$C$乘以$f(n)$，即$T(n) \leq C \cdot f(n)$。

$\Omega$符号则用于描述算法的最优时间复杂度，表示算法在输入规模趋近于无穷大时，其运行时间的增长速度不会低于一个固定的下界。具体来说，如果一个算法的最优时间复杂度为$\Omega(f(n))$，那么随着输入规模$n$的增加，算法的运行时间不会低于一个常数$C$乘以$f(n)$，即$T(n) \geq C \cdot f(n)$。

$\Theta$符号则表示算法的平均时间复杂度，它描述了算法在最好情况和最坏情况下的运行时间都相同时的时间复杂度。如果一个算法的平均时间复杂度为$\Theta(f(n))$，那么算法的运行时间随着输入规模$n$的增加而增长的速度与$f(n)$相同。具体来说，对于一个算法的平均时间复杂度为$\Theta(f(n))$，存在两个正常数$C_1$和$C_2$，以及某个正整数$n_0$，使得当$n \geq n_0$时，算法的运行时间在$C_1 \cdot f(n)$和$C_2 \cdot f(n)$之间。

因此，$O$符号、$\Omega$符号和$\Theta$符号都是用于衡量算法复杂度的标准符号，但它们的含义和使用方式略有不同。在分析算法的复杂度时，我们通常使用$O$符号来描述最坏时间复杂度，$\Omega$符号用于描述最优时间复杂度，而$\Theta$符号则更适合用于描述平均时间复杂度。

等式和不等式中的渐进记号

• 当渐近记号独立于等式（或不等式）的右边（即不在一个更大的公式内）时，如在$n=O(n^{2})$中，我们定义等号意指集合的成员关系：$n \in O(n^{2})$。

• 当渐近记号出现在某个公式中时，我们将其解释为代表某个我们不关注名称的匿名函数。

  • 按这种方式使用渐近记号可以帮助消除一个等式中无关紧要的细节与混乱。
  • 例如，公式$2^{2} + 3n + 1 = 2^{2} + \Theta(n)$ 意指 $2^{2} + 3n + 1 = 2^{2} + f(n)$ ， 其中$f(n)$是集合$\Theta(n)$中的某个函数。在这个例子中，假设$f(n)=3n + 1$，该函数确实在$\Theta(n)$中。

• 渐近记号出现在等式的左边，我们使用以下规则来解释这种等式：无论怎样选择等号左边的匿名函数，总有一种办法来选择等号右边的匿名函数使等式成立。

  • $2n^{2} + \Theta(n) =\Theta(n^{2})$
  • 我们的例子意指对任意函数$f(n) \in \Theta(n)$，存在某个函数$g(n) \in \Theta(n^{2})$，使得对所有的$n$，有$2n^{2}+ f(n) = g(n)$。
  • 换旬话说，等式右边比左边提供的细节更粗糙。

比较各种函数

实数的许多关系性质也适用于渐近比较。下面假定$f(n)$和$g(n)$渐近为正。

• 传递性
• 自反性
• 对称性
• 转置对称性